Bağdat'tan Kurtuba'ya ve oradan Semerkand'a kadar bütün şehir merkezlerinde sayısız kütüphanelerin ve binlerce ilim adamının on binlerce öğrenci okuttuğu herkes tarafından bilinir. Beytü'l-hikme içinde ve dışında yetişen ilim adamlarının en meşhur olanlarından Huneyn İbn Ishak başta olmak üzere Sabit İbn Kurre, Muhammed İbn Musa el-Harezmi, el-Battanî, Ebu Bekr er-Razî, Ebu'l-Vefa el-Buzcanî, İbn Sina, el-Birûnî ve sayamayacağımız kadar çok ilim adamı bütün dünyayı aydınlatacak ilmi çalışmalarını gerçekleştirmiş ve Avrupa aydınlanma çağına zemin hazırlamışlardı.
Bu önemli isimlerin içinde trigonometri ilminin kurucusu olan Ebu'l-Vefa el-Buzcanî, İslâm matematik ve astronomi âlimlerinin önde gelenlerinden olup "mühendis" ve "hâsib" lakaplarıyla da tanınır. Horasan'da Herat'la Nîşâbur arasında yer alan Bûzcân kasabasında 1 Ramazan 328'de (10 Haziran 940) doğdu ve 388'de (998) Bağdat'ta öldü; bazı kaynaklarda ölüm tarihi 387 (997) olarak geçer.
Ebu'l-Vefa el-Buzcanî, matematik alanında temel bilgileri amcası Ebû Amr el-Mugāzilî ve dayısı Ebû Abdullah Muhammed b. Anbese'den öğrendi. Daha sonra Bağdat'a giderek devrin tanınmış âlimlerinin yanında tahsilini tamamladı ve Bağdat'ta ders vermeye, matematik ve astronomi alanında araştırmalar yapmaya başladı. Özellikle rasatlarının çoğunu burada Büveyhî emîrlerinden İzzüddevle Bahtiyâr b. Muizzüddevle döneminde gerçekleştirdi.
PEYGAMBERİMİZİN FEYİZLİ VE BEREKETLİ ‘RAHLE-İ TEDRİS’İ: SUFFE
Bu konuda görüşlerinden faydalanmak için Bîrûnî ile mektuplaşıyordu; bu sırada Bîrûnî'nin Hârizm'de, Ebü'l-Vefâ'nın Bağdat'ta gözledikleri birküs olayının rasat sonuçlarını karşılaştırmışlardı. Ayrıca Bîrûnî bazı eserlerinde onun rasatlarından söz etmiştir. Ebü'l-Vefâ'nın, çağdaşı olan Ebû Ali el-Hubûbî ile de mektuplaştığı ve Hubûbî'nin üçgenlerin alanını bulma konusunda ondan bazı formüller istediği bilinir.
İbn Hallikân'a göre Ebü'l-Vefâ meşhur bir matematikçidir (hâsib) ve ayrıca geometri ilminde de özellikle kirişlerle ilgili yeni ve benzeri görülmemiş buluşların sahibidir. Kemâleddin İbn Yûnus da onu geometriyi en iyi bilen âlimler arasında gösterir.
Her ne kadar trigonometriyle ilk defa Me'mûn devri âlimlerinden Habeş el-Hâsib el-Mervezî ilgilenmişse de bu konuyu sistematik bir ilim dalı haline getiren Ebü'l-Vefâ'dır. Bu husustaki çalışmaları arasında trigonometri teoremlerinin ilk ispatlarını vermiş, "zıl" adı altında tanjantı, "kutr-ı zıl" adıyla sekantı tarif etmiş ve trigonometrik fonksiyonların yayın fonksiyonu olarak 15 dakikalık adımlarla hassas cetvellerini gerçekleştirmiştir.
BİLİMİNİN IŞIĞI YANGINIYLA SÖNMÜŞ 'İSKENDERİYE KÜTÜPHANESİ'
Bazı küresel üçgen problemlerinin çözümü için de çeşitli metotlar geliştirmiştir. Büyük harfler açıları, küçük harfler kenarları ve A dik açıyı göstermek üzere bir küresel dik üçgende -tgctgC = sin b, -tgbtgB = sin c eşitliklerini bulmuştur. Bunların yanında eğik açılı küresel üçgenler için sinüs teoremini de ispat etmiştir. Parabolün nokta nokta çizimi için yeni bir metot geliştiren Ebü'l-Vefâ'nın ayrıca geometrik çizimlerle ilgili kısmen Hint modellerine dayanan bazı önemli çalışmaları da vardır.
Pergelin bir tek açıklığıyla daire içine kare çizimini ve verilen bir kare içine eşkenar üçgen çizimini ilk defa Ebü'l-Vefâ yapmıştır. Ayrıca düzgün çokyüzlüler problemiyle uğraşmış, yedi ve dokuz kenarlı düzgün çokgenlerin yaklaşık çizimlerini vermiştir. Onun cebir ve denklemler teorisine de çeşitli katkıları vardır ve özellikle x4 + px³ = r denkleminin çözümünü iki parabolün ara kesitini alarak bulması dikkat çekicidir.
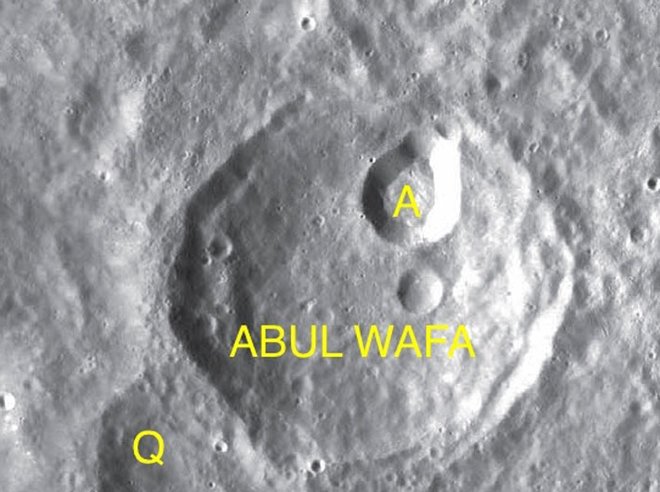
Ebü'l-Vefâ'nın astronomi çalışmaları arasında büyük önem taşıyan orijinal rasatlarla tesbit ettiği yeni parametreler asırlar boyunca kullanılmıştır. el-Mecistî adlı eserinde Danimarkalı astronom Tycho Brahe'den (ö. 1601) çok önce ayın değişimini de (tâdil, varyasyon) incelemiş ve Ebû Nasr İbn Irâk'ın eserlerini bazı noktalarda tenkit etmiştir. Bu konudaki görüşleri ve tanjantla ilgili buluşlarının orijinalliği XIX. yüzyıldan beri ilim tarihçileri arasında tartışılmaktadır. Astronomiye yaptığı büyük katkılardan dolayı ayın bir kraterine onun adı verilmiştir.
ESERLERİ
İbnü'n-Nedîm'in el-Fihrist'inde ayrıntılı bir listesi bulunan eserlerinin bir kısmı kaybolmuş, bir kısmı da henüz incelenmemiştir. Öklid ve Diophantus'un çalışmaları hakkındaki yorumlarıyla kendi orijinal buluşlarını ihtiva eden kitabı ve Ebû Ca'fer el-Hârizmî'nin cebir kitabına ait şerhi kaybolanlar arasındadır. Mevcut eserlerinin başlıcaları şunlardır:
ez-Zîcü'ş-şâmil
Çeşitli yazma mecmuaları arasında birçok nüshası bulunan eser. Tokatlı Seyyid Hasan b. Ali el-Kûmnâtî tarafından ez-Zîcü'l-kâmil adıyla şerhedilmiş ve Çelebi Sultan Mehmed'e ithaf edilmiştir. Süleymaniye Kütüphanesi'nde bir yazması bulunan bu şerhin başka bir nüshası da Paris Bibliothèque Nationale'de kayıtlı olan kitabın sonundadır. Esîrüddin el-Ebherî de bu esere bir şerh yazmıştır.
İSLAM ÂLEMİNE BÜYÜK EMEK VERMİŞ ÖMÜRLER
Kitâb fîmâ yehtâcü ileyhi'l-küttâb ve'l-'ummâl min 'ilmi'l-hisâb
Kâtiplere ve vergi memurlarına yardımcı olmak üzere 961'de Büveyhîler'den Adudüddevle adına kaleme aldığı bu kitap, her birine "menzil" adı verilen yedi bölümden oluşmuştur; bu sebeple esere Kitâbü Menâzilü's-seb' de denilmektedir. Her bölümü yine yedi babdan meydana gelen kitapta doğu İslâm ülkelerinde tüccarlar, kâtipler ve vergi memurlarının hesaplarında kullandıkları metotlar sistematik olarak düzenlenmiş, bayağı kesirlerin çözümü için orijinal ve pratik bir metot geliştirilmiştir. (10ª+b) (10ª+c) şeklindeki bir hesabın nasıl yapılacağını gösteren müellif, burada muhtemelen Hint matematiğinin de tesiriyle negatif sayıları "deyn" (borç) adı altında kullanmıştır. Bu eser Ahmed Selîm Saîdân tarafından 'İlmü'l-hisâbi'l-'Arabî adlı kitabının içinde neşredilmiştir.
Kitâb fîmâ yehtâcü ileyhi's-sâni'min a'mâli'l-hendese
990'da telif edilen, iki ve üç boyutlu birçok çizimin yer aldığı eser zanaatkârlar için hazırlanmış bir tür geometri kitabıdır. Çizimlerin bir kısmı Öklid, Archimedes, İskenderiyeli Heron, Theodosius ve Pagpus'tan alınmış olmakla birlikte verilen örneklerin çoğu orijinaldir. Bu eserin Uluğ Bey'in Kütüphanesi için istinsah edilmiş çok güzel bir nüshası Süleymaniye Kütüphanesi'nde olup S. A. Krasnova tarafından Rusça'ya çevrilmiştir.
Kitabın iki ayrı Farsça tercümesi bulunmaktadır ve bunlardan birinin önemli bir bölümünü Woepke Fransızca'ya çevirmiştir. Ayrıca Sâlih Ahmed el-Alî'nin yayımladığı (Bağdad 1979) eserin biri Kemâleddin İbn Yûnus (Arapça), diğeri Muhammed Bâkır Yezdî (Farsça) tarafından yapılan iki de şerhi vardır.
HAM İKEN ALLAH YOLUNDA YANAN MEVLÂNA CELÂLEDDÎN-İ RÛMÎ
el-Mecistî (Kitâbü'l-Kâmil)
Tamamı günümüze ulaşmayan eser, muhtemelen şimdiye kadar ele geçmemiş olan ez-Zîcü'l-vâzıh, adlı kitabının aynı veya bir kısmıdır. Eksik bir nüshası Bibliothèque Nationale'de bulunan kitabı L. A. Sedillot kısmen Fransızca'ya çevirmiş, Carra de Vaux da bir makalesinde inceleyerek tahlil etmiştir. XIX. yüzyılın başlarına kadar Ptolemaios'un Almagest'inin bir tercümesi sanılan el-Mecistî'nin yapılan incelemeler sonucunda orijinal ve önemli bir çalışma olduğu anlaşılmıştır. Kitapta yer alan başka konuların yanında özellikle astronomi, trigonometri ve ayın hareketi teorisiyle ilgili kısımlar dikkate değer niteliktedir.
Risâle fî terkîbi 'adedi'l-vefk fi'l-murabba'ât
Kare vefkler üzerine kaleme alınmış bir eserdir.
GELECEK NESİLLERE IŞIK TUTAN OSMANLI ÂLİMİ: BİRGİVÎ
Cevâbü Ebi'l-Vefâ' Muhammed b. Muhammed el-Bûzcânî 'ammâ se'elehü'l-fakıh Ebû 'Alî el-Hasan b. el-Hâris fî mesâhati'l-müselles
Ebü'l-Vefâ'nın, Ebû Ali el-Hubûbî'nin üçgenlerin yüzeyini hesaplamak için kendisinden istediği formülle ilgili cevabından ibaret olup tıpkıbasımı S. Kenedy ve Mustafa Mevâldî tarafından Mecelletü Târîhi'l-'ulûmi'l-'Arabiyye adlı dergide İngilizce ve Arapça tahliliyle birlikte yayımlanmıştır. (TDV,İslamansiklopedisi)